Given a set of numbers where the total count is unknown, describe an algorithm that can randomly select k numbers from this set such that each number has an equal probability of being selected.

If the set contains n numbers, then the probability of selecting each number is k/n. However, the challenge here is that the total count, n, is unknown. So how can we calculate the probability of selecting each number?

Reservoir Sampling Algorithm

Everyone is familiar with a swimming pool (reservoir). Some pools have flowing water, with both inlet and outlet pipes. After a volume of water equivalent to the pool’s capacity flows through, is all the water in the pool replaced? Of course not. Some water may stay in the pool for a long time, while some may flow out shortly after entering. Inspired by this phenomenon, the reservoir sampling algorithm was developed. The key to the reservoir sampling algorithm is to ensure that the water entering the reservoir and the water already in the reservoir have the same probability of remaining in the reservoir. Additionally, the reservoir sampling algorithm can solve such sampling problems in O(N) time complexity without knowing the total count in advance.

Core Principle

This section involves formulas, so to ensure clarity, an image is directly included.

Python Implementation

Next, let’s try implementing the reservoir sampling algorithm in Python. Since the reservoir sampling algorithm samples without knowing the total count in advance, we define a method to receive individual elements and place this method within a class to hold the sampled data.

import random


class ReservoirSample(object):

    def __init__(self, size):
        self._size = size
        self._counter = 0
        self._sample = []

    def feed(self, item):
        self._counter += 1
        # For the i-th element (i <= k), directly enter the pool
        if len(self._sample) < self._size:
            self._sample.append(item)
            return self._sample
        # For the i-th element (i > k), enter the pool with a probability of k / i
        rand_int = random.randint(1, self._counter)
        if rand_int <= self._size:
            self._sample[rand_int - 1] = item
        return self._sample

Test Code

Next, we implement a test case to verify whether the implemented algorithm is correct. Since it is random sampling, it cannot be verified through a single test, so we verify by executing multiple times. For example, randomly sample 3 numbers from 1-10, then execute the sampling 10,000 times. If the algorithm is correct, the number of times each number from 1-10 is sampled should be similar, around 3,000.

import unittest
from collections import Counter

from reservoir_sample import ReservoirSample


class TestMain(unittest.TestCase):

    def test_reservoir_sample(self):
        samples = []
        for i in range(10000):
            sample = []
            rs = ReservoirSample(3)
            for item in range(1, 11):
                sample = rs.feed(item)
            samples.extend(sample)
        r = Counter(samples)
        print(r)

if __name__ == '__main__':
    unittest.main()

The output result is as follows:

Counter({7: 3084, 6: 3042, 10: 3033, 3: 3020, 8: 3016, 5: 2997, 4: 2986, 2: 2972, 9: 2932, 1: 2918})

The output shows the number of times each number was sampled. The distribution can be clearly seen through a chart.

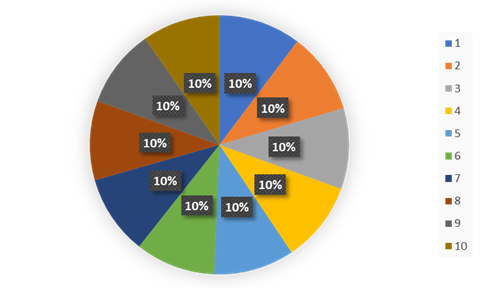
It can be seen that the reservoir sampling algorithm is very suitable for random sampling, as each element has the same probability of being sampled.

Code

The above algorithm and test code are available on Github and can be downloaded for use directly.